Gameinstance.com - Bass-Reflex phase corrector - IIR 2nd order digital filter

The fact that vented loudspeakers exhibit low frequency group delays is no longer news. For years we've been listening our favorite records through these things and we took for granted what they gave us. Unfortunately this isn't what we were supposed to hear but that's the price we payed for that extra bass.

In the attempt to correct this cause of distortion, this article presents a 2^nd order IIR filter with constant magnitude and variable phase applied on the reversed sampled audio array.

Originally proposed

by Herzog and Hilsamer, the solution addresses only the phase delay generated by the Helmholtz resonator by employing a digital biquadratic filter of the form:

H(z)=((1-1/re^(jomega_0)z^-1)(1+1/re^(-jomega_0)z^-1))/((1-re^(-jomega_0)z^-1)(1+re^(jomega_0)z^-1))

The transfer function has two complex conjugate poles with a 1/r modulus and two complex conjugate zeros with a radius of r. The r must be less than 1 to maintain the system stability but to achieve a near 0 dB gain, the filter has to use a value close to 1. However, r is the tuning parameter for the phase shift as well and so the value best matching a certain setup has to be determined by trial and error.

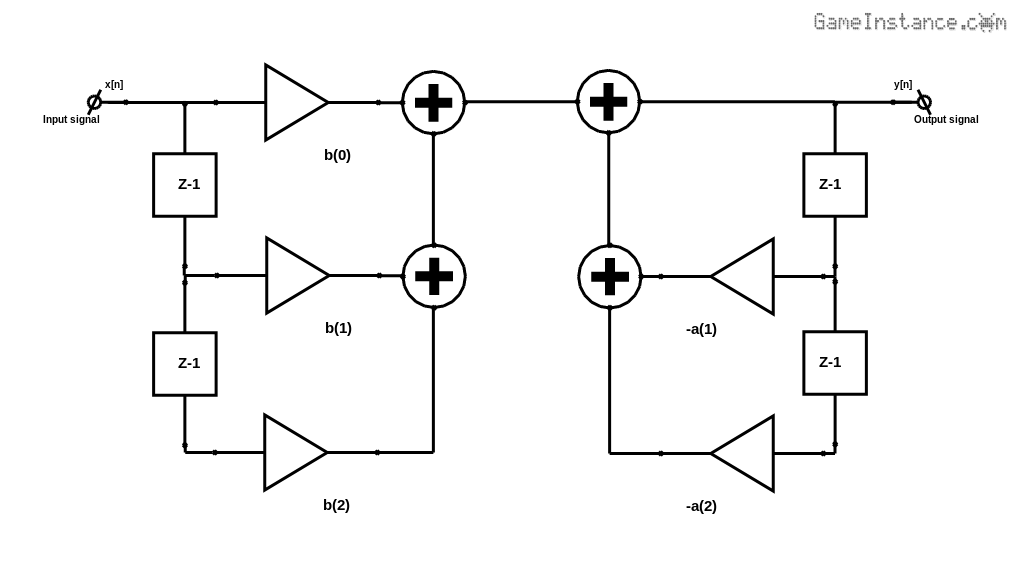Direct form implementation of the vented box phase correction IIR filter.

To proceed with the implementation, one must extract the b_N and a_N coefficients. For that the relation needs to be processed further more: removing the paratheses, grouping terms with similar z^-N and, finally, applying Euler's formula.

B(z)=1-2jsin(omega_0)/rz^-1-1/r^2z^-2

giving

a_0=1

a_1=-2jsin(omega_0)/r

and

a_2=-1/r^2

A(z)=1+2rjsin(omega_0)z^-1-r^2z^-2

also giving

a_0=1

a_1=2rjsin(omega_0)

and

a_2=-r2

Substituting ω₀=2πω_b/ω_s, where the ω_b is the box tuning angular frequency and ω_s the sampling angular frequency of the audio signal, gives the complex coefficients of our IIR filter.

The python sketch

using the tuning frequency of the Classix II for a signal sampled at 44.1 kHz looks like this:

from scipy import signal
from scipy.io import wavfile
import math
import numpy as np
from pydub import AudioSegment

song = AudioSegment.from_mp3("/path/to/input/signal.mp3")
samples = song.get_array_of_samples()
samples = np.array(samples)
reversed_input_signal = samples[::-2]

# the filter parameters
fb = 40
fs = 44100
w = 2 * math.pi * fb / fs
r = 0.99

# IIR coefficients
b = [1, -2j / r * math.sin(w), - 1 / (r**2)]
a = [1,  2j * r * math.sin(w), - (r**2)]

# applying the filter on the reversed audio sequence
reversed_output_signal = signal.lfilter(b, a, reversed_input_signal)

reversed_output_signal = np.asarray(reversed_output_signal, dtype=np.int16)
output_signal = reversed_output_signal[::-1]
wavfile.write('out_signal.wav', fs, output_signal)

The test audio sample is a stereo MP3 file. Therefore the samples[::-2] extracts only one channel and performs a negative step iteration to reverse the input array. The rest of the code should be self explanatory.

Listening impressions

If you don't know what to expect, it's likely you won't notice any difference. Group delay correction isn't something as obvious as, say, a linear frequency response. The subtle improvement becomes evident for rhythmic instrumental recordings where piano, drums or higher pitch instruments play along with double bass. Listening closely both the filtered and original versions, you will remark that the orchestra is better synchronized or that the bass keeps up the beat.

Remember, nonetheless, that the filter takes the input signal in reverse. The obvious down-side is that the method cannot be applied for live audio signals. This new issue can be addressed as well but not without further compromises. However, this is beyond the scope of this article.